EVALUATION METRICS 

Here first we need to learn. how the evaluation metrics is going to help in model building process. To explain it i am gonna take a real life example when we are a child we use to go school.where our teacher teach us deliver the lecture and provide the class notes and take our test to check how much we understand the topic and to check  the ability of the understanding of every student into the class so here we also do same thing we have a data set we will divide it into 2 part one is the train and other is the test part. train data set is consider as our teacher lecture and test part is consider as our exam's so that's why we make this Evaluation metrics to check the quality of our model .

Confusion matrix:- 

A confusion matrix is the n*n matrix where n represent the number of classes in the variable in the titanic data set our dependent variable is only having two classes 1 = survived and 0 = not survived so in this cause the value of the n  = 2 and the confusion matrix form is 2*2 matrix 

now the row in this matrix is Actual  value  and the column in this matrix represent the prediction value

as you can see in this image  

  

TP = the value which is actually positive and also predicted positive 

FP  = the value which is actually negative but predicted positive \

FN = the value which is actually negative but it is predicted positive 

TN = the value which is actually negative and we also predict it negative 

we use this matrix to evaluate our model 

Accuracy:- this is the first and most popular evaluation matrix trick used for evaluation task 

it is the ratio of correct predicted values over the total predicted values.

it is pretty state forward the correct predicted value divided by the the total predicted value 

in reality accuracy as an evaluation on an unbalance data is not consider god and also it is called as it's limitation 

Alternative To the Accuracy Metric 

True positive rate:- Ratio of actual positive prediction over total actual positives 

False Negative Rate :- Ratio of actual positive, predictive as negative; over total actual positive 

True negative rate : Ratio of actual negative prediction over the total negative 

False Positive Rate:- Ratio of actual negative predicted as positive; over total actual negative 

 

we derived 4 matrix from the confusion matrix 

in any given model TRP is always desireable higher the true positive rate better is the model also the lower the value of FNR better the model 

Precision and recall 

Precision :- it is defined as the ratio of all the positive predictions, hoe many actually positive 

precision is used when we cannot afford to have false positive value or avoiding false positive is more important than encountering false negative 

 Recall : - it can be defined as out of total actual positive value, hoe many have been predicted as positive 

recall is use when we can not afford false positive  or avoiding false negative is priorities over encountering false positive 

• high Precision, Low Recall 
• high Recall, Low precision 
• Choice depends upon the cause that which one is used 
• Combined use F1 score 
• F1 is maximum when precision = recall 

 so far we use the predictive classes of value 0,1 what if we have the probability of classes and not the classes them self and we need to use  this probability value to check how my model perform 

 

 than we need to set a markdown that the value lies under 0.5 is consider as 0 and the value above than or equal to 0.5 is consider as 1 after that we can use all the metrices to predict the right value if our prediction value not satisfy our condition than we need to change it and set some threshold value in the place of changing the model we change the threshold value is called as thresholding 

AUC-ROC:- 

AUC = area under the curve 

ROC = receiver operating Characteristic

ROC is originally used for distinguishing 'noise' from 'not noise' but in machine learning used for Evaluation Metric for binary classification 

give trade of between true positive and false positive 

 

Problem  with AUC-ROC 

• Consider only the order of probability because of this 
• can't use to compare the two models 
• to overcome this limitation we have an another metric names as log loss 

Log Loss 

it is the negative average of the log of corrected predicted probabilities for each instance.

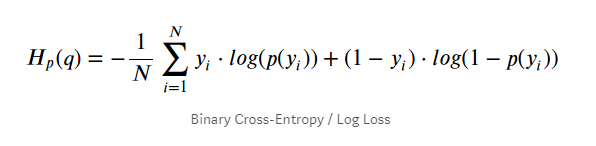
• p(yi) is the probability of 1 
• 1-p(yi) is the probability of 0 

Evaluation Metrics : Regression 

• Mean Absolute Error

 

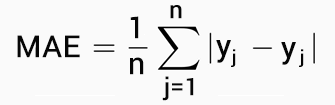
• Mean Squared Error :- in this value we square the value of error to avoid the negative value but it have a problem when we square the value it will change the unit of the error foe example if we have the error in meter id we square it will converted in meter square

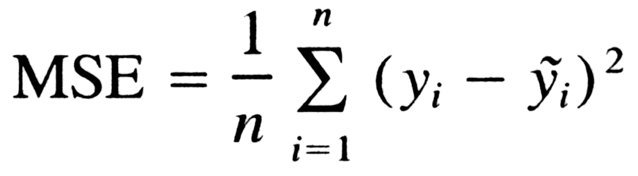
• Root Mean Squared Error:-  so to compensate the limitation of Mean square error  we can take the root of the error and come back at our exact unit which is called as root mean square error 

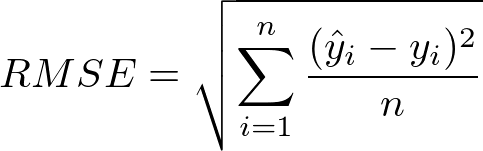
this is more often used in machine learning and the data science but it is not the best metric for the regression problem's RMSE basically use the difference of the error so it might be wrong in some place to overcome this limitation we use RMSLE

• Root Mean Squared log Error :- this bascially scale down the larger value 

• R-squared:- in cause of classification problem of the accuracy is 0.8 we can compare with it random model the accuracy of which is 0.5 so random model here is treated as bench mark but when we talk about  MSE and RMSE matrix we don't have a bench mark to compare we can use MSE  value we generated last instied of using it alone we use it by dividing by MSE(baseline) model 

baseline model :- it is a simply MSE where the predicted value is simply replaced by mean of all value 

as we can say as MSE decreases our model performance is increase which is quite contradictory to the general idea that higher value are better so that we simply squared relative square error with 1 

R- squared either increases or does not change 

• Adjusted r-squared

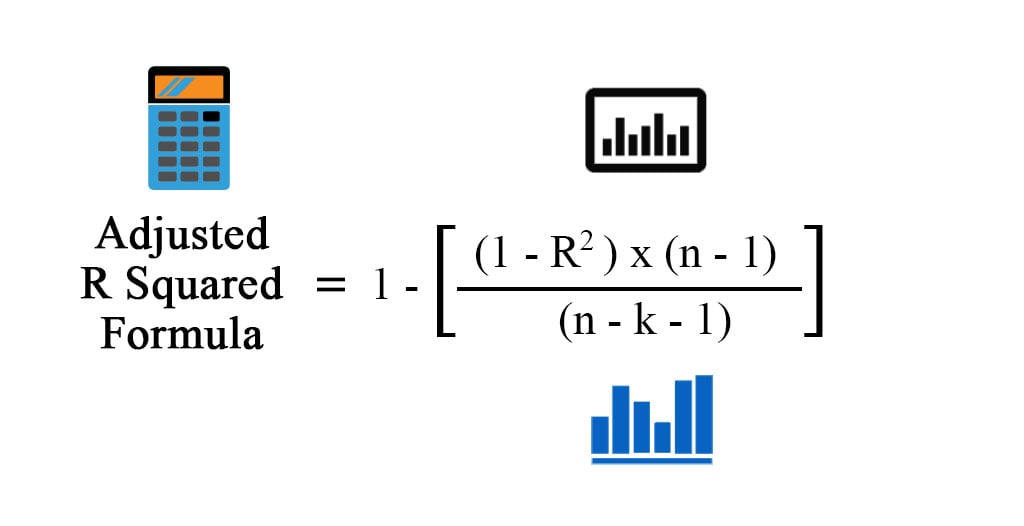
n = number of samples 

k = number of features 

now if we add the new feature the term in denomenator increases it means whole fraction increases