Underfitting and Overfitting
Under fitting and Over fitting
sum up and all this thing with the real life example we have the a class in which three student are present
and its a math class
Student 1 = don't pay much attention in the class
Student 2 = Learn all the answer in the class rather than under standing the concept what is taught by the teacher
Student 3 = Understand the concept behind the every question which is taught by the teacher
after the class teacher take the test of every student all the student score different score in test
teacher put all the same questions in the test which is taught in class
student 1 = as they don't pay attention in the class by random guessing he scored 50% marks
Student 2 = as they remember all the question taught by the teacher in the class he scored 98% pretty good score in the class
Student = 3 as he is problem solver he under stand what is taught by the teacher in the class and score a decent score of 92%
after the first test now teacher want to know that the students understand the concept behind the question she change all the question but the concept behind the questions are same
Student 1 = again as he don't pay much attention in the class by random guessing he scored 48%
Student 2 = as he cramp all the question rather than understanding the concept behind the question so he was confused because the statement of the questions are change and scored 68% in the class
Student 3 = as he is a problem solver understand the concept behind the question he scored 89% in the test pretty decent score
Now lets compare it with this with our problem
1.student 1
score in test1 = 50%
score in test2 = 48%
is the perfect example of under fitting because he don't put much attention in the class and just give answer's by random guessing
2.Student 2
score in test 1 = 98%
score in test 2 = 68%
this is the best example of over fitting because it show awesome result in the first test and not good result in the second one as we can compare if some our algorithm perform good in training data but not perform good on the test data
3. Student 3
score in test 1 = 92 %
score in test 2 = 89%
this is the best example of the optimize Algorithm because in this they perform both in the training and test our result is pretty decent and consistent
Implementation on the Jupyter notebook:-
Validation:-
we know what is over fitting under fitting and best fitting model means
now the question arise here will the best fit model work on the completely unseen data.....?
we said yes on this question
let us think about it first of all we need to truly understand what unseen data is so far we are using the test set for the unseen data but is it really unseen in the notebook we seen earlier we select the optimum value of k based on it performance based on it training and test data the model actually had a look on the test data it is not Truly unseen we are looking at the model performance on the test data to decide the optimum value of k this means we are not testing the performance on the completely new data our model might fail in that cause
we need a data set to build and implement any machine learning model we divide this data into 2 part called as test and train data so far we are optimizing the model on the base of test data we need to have some data which is completely unknown to the model. so from the remaining training data we form a another data set called as validation data set we keep this test set for the final evaluation only.
- Hold out validation:- it divide the data in such a manner that the train set and validation set have equal distribution of target variable
limitation :- in hold out validation we need good chunk of data kept aside but it cause a problem
when we are working on a small data but we capture to required a complex relation
Implementation of hold out validation on jupyter notebook:-
- K Fold Cross Validation :-
- Shuffle the data set randomly
- Split the data into k groups
- pick a group as a hold out
- take the remaining groups as training and fit a model
- predict and evaluate on the hold out
Advantages
- Not required to place a data aside
- Prevents over fitting
- Consistency of model
Deciding K
- 5<k<10: generally
- Validation size = statistically significant
- k = 2 , 50-50 split , high bias
- k>10, more data for training. More models
- k = number of observation extreme case Also known as leave one out.
- Leave one out cross Validation :-
- N instances n models
- not significant when the size of data is very large
- best practice for small data set
- Can use leave 'p' out validation
Implementation on the Jupyter notebook:-
Bias and Variance in Predictive Modelling
- High bias :- in this our model are very simple we are not able to capture the available signal of the data on the basics of this simple assumptions the model is under fitting and the value of 21>k and also the complexity of the model is low
- high variance :- in this model is two bias it will capture the noise along the signal decision boundaries get very sensitive to the training point and trying to capture every single instance on the data set . in this cause model have very high variance and we called this type of model Over fit model in this cause the value of k <10 and also the model is very complex
- optimum :- it is an ideal cause in which we are in between of high bias and high variance model it generalize data set Optimally while avoiding the noise this is called as Best fit model the value of k is in between 12<k<21 and the complexity is optimum
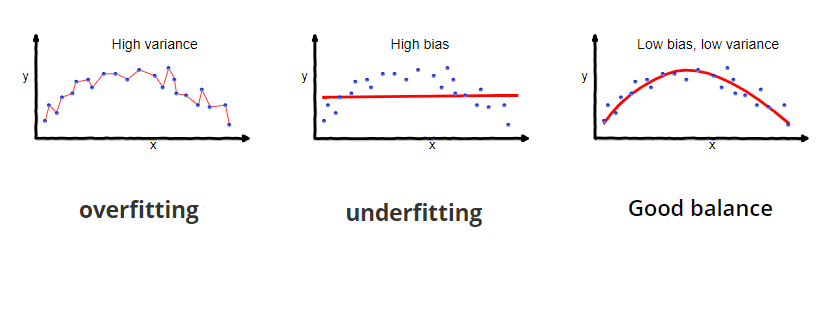
Bias and Variance Trade off
- strong trade off
- High Variance => Low Bias
- high bias=>Low Variance
- optimum in between
- complexity where bias and Variance error are low together

Comments
Post a Comment